Julia Intro

2018-11-07 Programming

Juliaet, Wherefore art thou?

As Yoda once said…

> YAPL - yet another programming language. Learn something new, you must.

Why Learn Julia?

Julia was designed from the beginning for high performance. Julia programs compile to efficient native code for multiple platforms via LLVM. As such, it’s an interesting programming language to take a look at as it’s a serious contender for certain classes of programming problems; most notibly, scientific and data-centric analysis.

In this blog post, I’ll take a look at some of the interesting features as well as an implementation of displaying Mandelbrot fractals using Julia.

Julia features worthy of note

As with all languages, a good starting point is the documentation. Take a tour of the items on the left-hand menu and you’ll see many of the traditional elements of most contemporary programming languages. Some notable sections to look at are:

Complex and Rational Numbers
Metaprogramming
Noteworthy Differences from other Languages
Base
Standard Library

Let’s take a look some of the features above by way of examples.

Going beyond the int/float types

Every language implements basic primitive data types like integers int and floats floats. But some languages go a step further and implement numbers that are slightly more abstract like Complex and Rational, complex and rational numbers, respectively. Let’s take a closer look at complex numbers in julia.

A complex number, $c$ is a number that has a real and imaginary component: $c = a + bi$, where both $a$ and $b$ are Real numbers. Moreover, real numbers are represented as Floats. There are several ways to make a Complex number is julia.

# create a complex number whose real component is 2.0 and imaginary component is 3.0
c = 2.0 + 3.0im

Another way to create a Complex number is to use the constructor.

c = Complex(2,3)
d = ComplexF64(2,3)
e = ComplesF32(3,4)

Notice that the default constructor creates a complex number comprised of 64-bit floats. We can explicitly create a 64 or 32-bit float complex as well.

Obligatory application of Complex Numbers: Fractals!

An exciting application of complex numbers is the construction of Fractals - specifically Mandelbrot and Julia sets.

Let’s create an image of the Mandelbrot set in Julia! We’ll generate a jpeg file of the Mandelbrot set. The Mandelbrot set is calculated by computing the escape iteration of points in the complex-plane. So in order to do so we need to iterate of the real and complex dimensions and compute the escape value at each point. Based of the value of the escape iteration, we’ll color that cartesian point on the complex plane. The resulting image is a visualization of the Mandelbrot set bounded by the selected rectangle in the complex plane.

A little math is required to further illustrated the point.

$$ z_{n+1} = z_{n}^2 + c $$

Where $z = 0, and c \in C, \text{where C(re,im) }re = [-2.50, 1.50], im = [-1.25, 1.25] $.

Translating that into a calculation looks like the following:

function mandel(c, maxiter::Int64)
    z=0+0im
    for n = 1:maxiter
        if abs(z) > 2
            return n-1
        end
        z = z^2 + c
    end
    return maxiter
end

We calculate the mandel(c) at a point c by first setting z to zero. Then we iterate up to the maxiter count. If the absolute value of z exceeds 2 we’ve escaped. Otherwise, we (recursively) calculate a new z-value using the recursive equation $z_{n+1} = z_{n}^2 + c$. if we never achieve an $abs(z) \gt 2$, then we return the maxiter.

Okay, so we now how to calculate the escape value at any point in the complex region, but how do we use this function to calculate our image? We first need to add a helper function that gives us Complex numbers in the region between the $min$ and $max$ values in our interval on the real and imaginary lines, respectively.

Let’s create a function that takes a minimum, maximum, and width. Our function will return an array containing width elements starting with minimum and ending with maximum and are uniformly distributed between these two points.

function float_range(xmin, xmax, width)
        r = Array{Float64, 1}(undef, width)

        delta = abs(xmax - xmin)/(width - 1)

        for i = 1:width
                r[i] = xmin + (i-1)*delta
        end

        return r
end

For example, if we wanted an array of 10 elements starting with -0.5 and ending with 0.5, we’d call our function like float_range(-0.5, 0.5, 10) resulting in an Array:

julia> float_range(-0.5, 0.5, 10)
10-element Array{Float64,1}:
 -0.5                
 -0.3888888888888889 
 -0.2777777777777778 
 -0.16666666666666669
 -0.05555555555555558
  0.05555555555555558
  0.16666666666666663
  0.2777777777777777 
  0.38888888888888884
  0.5

Using our range function, we can create a range of numbers both across the real and imaginary intervals. And then we can iterate across the two-dimensional interval, create a complex number, calculate the mandel(c) of that number and transform the max-iteration value into a color. Let’s take a look:

function mandelbrot_set(xmin,xmax,ymin,ymax,width,height,maxiter)
    r1 = float_range(xmin, xmax, width)
    r2 = float_range(ymin, ymax, height)

    cartesian =  Array{Float64, 3}(undef, 3, height, width)

    for y = 1:height, x = 1:width
        point = mandel(ComplexF64(r1[x], r2[y]), maxiter)
        if point == maxiter
                point = 0
        else
                point /= convert(Float64, maxiter)

        end

        red_color, blue_color, green_color = 1.0, 1.0, 1.0
        if point < 0.01
            red_color, blue_color, green_color = 1.0, 1.0, 1.0
        else
            red_color = point * 0.80
            blue_color = point * 0.80
            green_color = point * 0.15
        end

        cartesian[1,y,x] = red_color
        cartesian[2,y,x] = blue_color
        cartesian[3,y,x] = green_color
    end

    return cartesian
end

Our mandelbrot_set function will return an RGB array of height and width dimensions, Array{Float64,3}. So, we can take this array and create our jpeg image:


using Images
using FileIO

# load our mandel functions
include("mandel.jl")

# set parameters
h = 2500
w = 5000
iter = 10000

# time measurements
print("starting...\n")
tStart=time()

m_set = mandelbrot_set(-2.5,1.5,-1.25,1.25,w,h,iter)

tStop = time()

# write the image-file
img = colorview(RGB, m_set)
save("mandel.jpg", img)

print("done. took ", tStop-tStart, " seconds\n");

Take a look at our picture!

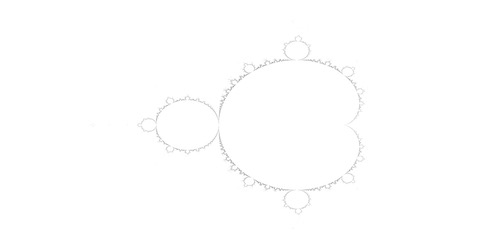
mandelbrot

Press here for a full-size image

The git repo is avaiable. Fork it and see what you can do! – enjoy! Next we’ll dive into meta-programming in Julia